最近,微软亚洲研究院发布了一种创新算法rStar-Math。它通过代码增强CoT、蒙特卡洛树搜索等,可以帮助小参数模型在不依赖老师模型蒸馏的情况下,实现多轮自我思维深度进化,极大增强模型的数学推理能力。

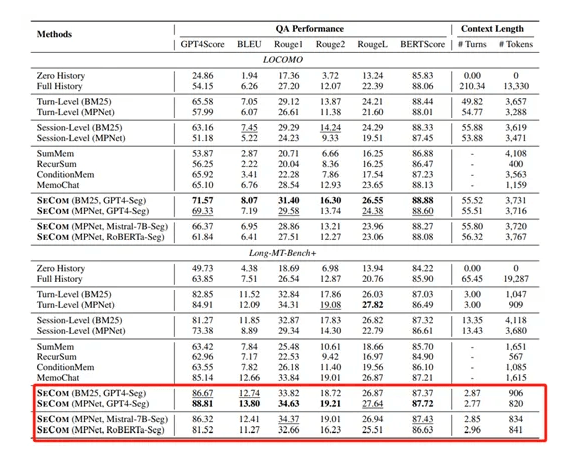
rStar-Math在美国数学竞赛AIME 2024测试中超过了OpenAI o1-preview的44.6%,以及所有其他开源的大模型。在MATH基准测试中,rStar-Math将阿里开源的小模型Qwen2.5-Math-7B的准确率从58.8%提高到90.0%,Qwen2.5-Math-1.5B的准确率从51.2%提高到87.8%,Phi3-mini-3.8B从41.4%提高到86.4%,全部超过了OpenAI o1-preview。
rStar-Math的特色介绍
1、代码增强CoT
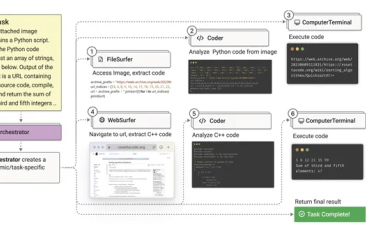
rStar-Math使用代码增强CoT(Chain-of-Thought,思维链)的方法,模型在生成每一步推理时,不仅生成自然语言的解释,还生成对应的Python代码,并通过代码执行来验证推理步骤的正确性。代码增强CoT能够提供严格的验证机制,确保每一步推理的正确性。
2、蒙特卡洛树搜索MCTS
为了进一步确保推理步骤的质量,rStar-Math使用了蒙特卡洛树搜索(MCTS)来生成逐步推理轨迹。MCTS被用来分解复杂的数学问题为多个单步生成任务。每个步骤中,策略模型生成多个候选步骤,并通过代码执行来过滤有效节点。通过广泛的MCTS回滚,rStar-Math能够为每个步骤分配Q值,确保生成的推理轨迹由正确且高质量的中间步骤组成。
3、PPM训练方法
rStar-Math通过引入过程奖励模型(PRM)来帮助模型找到更优的推理路径。PPM的核心思想是通过构建步骤级的正负偏好对来训练模型,而不是直接依赖于精确的步骤级评分。PPM的训练方法利用了MCTS生成的Q值,这些Q值是通过广泛的回滚和反向传播过程计算得出的,反映了每个步骤对最终答案的贡献。虽然这些Q值本身并不完全精确,但它们能够可靠地区分高质量步骤和低质量步骤。
PPM从MCTS树中选择Q值最高的两个步骤作为正例,Q值最低的两个步骤作为负例,构建偏好对。通过这种方式,PPM能够学习到哪些步骤更有可能引导模型生成正确的推理轨迹,从而在推理过程中做出更优的选择。
PPM的训练过程采用了标准的Bradley-Terry模型和成对排序损失函数。对于每个步骤,PPM预测一个奖励分数,并通过成对排序损失函数来优化模型的预测能力。成对排序损失函数的核心思想是最大化正例步骤与负例步骤之间的奖励分数差异,从而确保模型能够准确地区分高质量和低质量的推理步骤。
PPM的训练方法还引入了一个重要的创新点,避免直接使用Q值作为奖励标签。虽然Q值能够提供一定的步骤级反馈,但由于其固有的噪声和不精确性,直接使用Q值作为训练目标会导致模型学习到不准确的奖励信号。
4、rStar-Math通过四轮自我思维深度进化,并结合PPM、MCTS和代码增强CoT逐步增强模型的推理能力。
第一轮,通过监督微调对基础模型进行初步改进,为后续的自我进化奠定基础。这一轮的关键在于生成高质量的初始训练数据,并利用这些数据对基础模型进行微调。
第二轮,通过PPM显著提升模型推理能力。PPM通过分析策略模型生成的推理步骤,识别出哪些步骤是高质量的,哪些步骤需要改进。然后将这些反馈信息传递给策略模型,指导其在后续的推理中做出更好的选择。
第三轮,通过PPM增强的MCTS生成更高质量的数据,进一步提升模型的推理能力。在这一轮中,PPM不仅评估策略模型生成的推理步骤,还指导MCTS的搜索过程,使其更有效地探索高质量的推理路径。
第四轮,通过增加MCTS回滚次数解决超难数学推理问题。在前三轮自我进化的基础之上,第四轮自我进化通过增加MCTS的回滚次数,进一步提升了rStar-Math解决具有挑战性数学问题的能力。